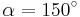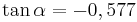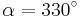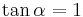Abbildungen im Koordinatensystem: Unterschied zwischen den Versionen

Version vom 10. Juni 2010, 10:47 Uhr

Lernpfad-Navigator

Abbildungen im Koordinatensystem

Arbeitsauftrag

Hier geht es nicht um die Eigenschaften der Abbildungen, die solltest du schon eine Weile kennen und kannst sie auch in der Formelsammlung nachschlagen. Stattdesssen solltest du Bildpunkte mit Hilfe von Abbildungsmatrizen berechnen können. Die Rechnung mit Matrizen wird nochmal erklärt, anschließend wird die Parallelverschiebung als erste Abbildung verdeutlicht.|} {{#slideshare:parallelverschiebung-100609155245-phpapp01}}

Leerzeile

Aufgaben

Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!

	Aufgabe 1 Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt.

$\sin \alpha=0,707 \quad$	$\quad \alpha=315^\circ$	$\quad \alpha=225^\circ$
$\cos \alpha=\frac{1}{2}$	$\quad \alpha=60^\circ$	$\quad \alpha=300^\circ$
$\cos \alpha=-0,866 \quad$	$\quad \alpha=210^\circ$	$\quad \alpha=150^\circ$
$\tan \alpha=-0,577 \quad$	$\quad \alpha=210^\circ$	$\quad \alpha=330^\circ$
$\tan \alpha=1 \quad$	$\quad \alpha=45^\circ$	$\quad \alpha=135^\circ$

Leerzeile

	Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können.

Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile

Abbildungen im Koordinatensystem

Abbildungen im Koordinatensystem: Unterschied zwischen den Versionen

Version vom 10. Juni 2010, 10:47 Uhr

Abbildungen im Koordinatensystem

Aufgaben

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge

@@ Zeile 24: / Zeile 24: @@
 | width="1000" style="text-align:left"| '''Arbeitsauftrag'''
 --------
-Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch!
+Hier geht es nicht um die Eigenschaften der Abbildungen, die solltest du schon eine Weile kennen und kannst sie auch in der Formelsammlung nachschlagen.
-|}
+Stattdesssen solltest du Bildpunkte mit Hilfe von Abbildungsmatrizen berechnen können. Die Rechnung mit Matrizen wird nochmal erklärt, anschließend wird die Parallelverschiebung als erste Abbildung verdeutlicht.|}
 {{#slideshare:parallelverschiebung-100609155245-phpapp01}}