Abbildung durch Achsenspiegelung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 24: | Zeile 24: | ||
| width="1000" style="text-align:left"| '''Arbeitsauftrag''' | | width="1000" style="text-align:left"| '''Arbeitsauftrag''' | ||
-------- | -------- | ||
| − | Die Achsenspiegelung ist eine grundlegende Abbildung, die du seit der sechsten Klasse kennt. Jetzt kannst auch Achsenspiegelungen an Ursprungsgeraden berechnen:|} | + | Die Achsenspiegelung ist eine grundlegende Abbildung, die du seit der sechsten Klasse kennt. Jetzt kannst auch Achsenspiegelungen an Ursprungsgeraden berechnen: |
| + | |} | ||
{{#slideshare:achsenspiegelung-100609155221-phpapp02}} | {{#slideshare:achsenspiegelung-100609155221-phpapp02}} | ||
<poem> | <poem> | ||
| − | <ggb_applet height="600" width=" | + | Hier kannst du Achsenspiegelung mit ihren Eigenschaften ausprobieren. |
| + | <ggb_applet height="600" width="850" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Achsenspiegelung.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 35: | Zeile 37: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | + | In Prüfungen werden von x abhängige Punkte abgebildet, hier ein Beispiel aus einer Prüfung. | |
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| − | | width="1000" style="text-align:left" style="background-color:#FFBBFF;"| '''Aufgabe 1 [[Bild: | + | | width="1000" style="text-align:left" style="background-color:#FFBBFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | + | Abbilden eines Punktes <math>\quad B_n</math>. (Abschlussprüfung 2007; Wahlteil ; B2). | |
| + | ------------ | ||
| + | Der Punkt <math>\quad A(-2|-2)</math> ist gemeinsamer Eckpunkt von Rauten <math>AB_nC_nD_n</math>. Die Eckpunkte <math>\quad B_n(x|-3x^{-1}-1)</math> liegen auf dem Hyperbelast k mit der Gleichung y=-3x^{-1}-1. Die Punkte <math>\quad C_n</math> liegen auf der Geraden g mit der Gleichung y=x. | ||
|} | |} | ||
| − | |||
| − | {| | + | {| |
| − | + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | |
| − | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="850" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Aufgabe_Hyperbelast.ggb"/> | |
| − | | | + | </popup> |
| − | | | + | |} |
| − | | | + | |
| − | | | + | {| border="1" |
| − | + | |Ermitteln Sie rechnerisch die Koordinaten der Punkte <math>\quad D_n</math> in Abhängigkeit von der Abszisse x der Punkte <math>\quad B_n</math> | |
| − | + | {| | |
| − | + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |
| − | + | |<popup name="Tipp"> | |
| + | Nutze die Symmetrieeigenschaften von Rauten aus! | ||
| + | </popup> | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: <math>\quad D_n </math> ({ -3x _5}<math>\quad ^{-1}</math>|{ x _5}) | ||
| + | </quiz> | ||
|} | |} | ||
| − | |||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
{| border="1" | {| border="1" | ||
| − | + | |Bestimmen Sie die Gleichugen des Trägergraphen h der Eckpunkte <math>\quad D_n</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | { | + | { |
| type="{}" } | | type="{}" } | ||
| − | + | Lösung: h: y={ -3/(x+1) _9} (Gebe einen Bruch mit / als Bruchstrich ein) | |
| − | + | ||
| − | Lösung: | + | |
| − | + | ||
| − | + | ||
| − | + | ||
</quiz> | </quiz> | ||
| + | |} | ||
| Zeile 82: | Zeile 84: | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Weiter gehts zu [[ | + | '''Weiter gehts zu [[Weitere Abbildungen]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
Version vom 11. Juni 2010, 08:30 Uhr
Abbildungen im Koordinatensystem
| Arbeitsauftrag
Die Achsenspiegelung ist eine grundlegende Abbildung, die du seit der sechsten Klasse kennt. Jetzt kannst auch Achsenspiegelungen an Ursprungsgeraden berechnen: |
{{#slideshare:achsenspiegelung-100609155221-phpapp02}}
Hier kannst du Achsenspiegelung mit ihren Eigenschaften ausprobieren.
Leerzeile
Aufgaben
In Prüfungen werden von x abhängige Punkte abgebildet, hier ein Beispiel aus einer Prüfung.
Ermitteln Sie rechnerisch die Koordinaten der Punkte 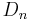 in Abhängigkeit von der Abszisse x der Punkte in Abhängigkeit von der Abszisse x der Punkte 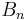
|
Leerzeile
Bestimmen Sie die Gleichugen des Trägergraphen h der Eckpunkte 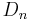 . .
|
Leerzeile
Weiter gehts zu Weitere Abbildungen
Leerzeile
Abbildungen im Koordinatensystem
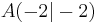 ist gemeinsamer Eckpunkt von Rauten
ist gemeinsamer Eckpunkt von Rauten 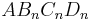 . Die Eckpunkte
. Die Eckpunkte 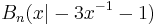 liegen auf dem Hyperbelast k mit der Gleichung y=-3x^{-1}-1. Die Punkte
liegen auf dem Hyperbelast k mit der Gleichung y=-3x^{-1}-1. Die Punkte 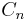 liegen auf der Geraden g mit der Gleichung y=x.
liegen auf der Geraden g mit der Gleichung y=x.

