Weitere Abbildungen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 29: | Zeile 29: | ||
<poem> | <poem> | ||
| − | <ggb_applet height="600" width=" | + | Im folgenden GeoGebra-Applet kannst du dir nocheinmal die Zentrische Streckung mit ihren Eigenschaften erarbeiten. |
| + | <ggb_applet height="600" width="850" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Zentrische_Strekung.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 62: | Zeile 63: | ||
</quiz> | </quiz> | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 87: | Zeile 68: | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Weiter gehts zu [[ | + | '''Weiter gehts zu [[Prüfungsaufgaben]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
Version vom 11. Juni 2010, 08:51 Uhr
Lernpfad-Navigator
Weitere Abbildungen
| Arbeitsauftrag
Es gibt noch weitere Abbildungen, die du bereits berechnen kannst,wie Orthogonale Affinität und Zentrische Strekung. Auch deren Abbildagleichungen sind noch einmal dargestellt. |
{{#slideshare:weitereabbildungen-100609155242-phpapp01}}
Im folgenden GeoGebra-Applet kannst du dir nocheinmal die Zentrische Streckung mit ihren Eigenschaften erarbeiten.
Leerzeile
Aufgaben
Es folgen nun Teilaufgaben aus ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigen.
Stellen Sie die Koordinaten der Punkte 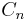 in Abhängigkeit der Abzisse x der Punkte in Abhängigkeit der Abzisse x der Punkte 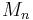 dar. dar.
|
Leerzeile
Weiter gehts zu Prüfungsaufgaben
Leerzeile
Abbildungen im Koordinatensystem
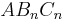 bilden eine Dreiecksschar mit dem gemeinsamen Punkt
bilden eine Dreiecksschar mit dem gemeinsamen Punkt 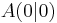 . Auf der Geraden g mit der Gleichugn
. Auf der Geraden g mit der Gleichugn 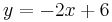 liegen die Mittelpunkte
liegen die Mittelpunkte 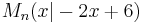 der Hyptenusen
der Hyptenusen ![\quad[AB_n]](/images/math/7/8/9/7897709debcde617572554254fb5973c.png) .
.
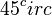 und dann eine zentrische Streckung um
und dann eine zentrische Streckung um 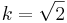 .
.
