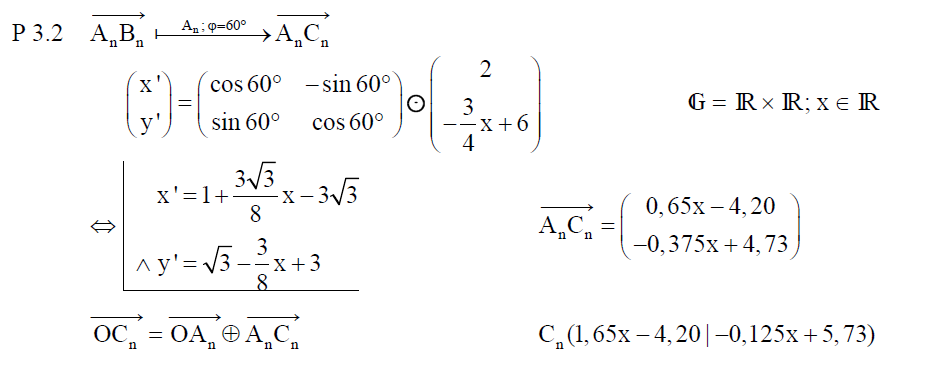Abbildung durch Drehung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 30: | Zeile 30: | ||
<poem> | <poem> | ||
Das Geogebra Applet zeigt dir nochmal die Abbildung Drehung. | Das Geogebra Applet zeigt dir nochmal die Abbildung Drehung. | ||
| − | <ggb_applet height="600" width=" | + | <ggb_applet height="600" width="900" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Drehung.ggb" /> |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 52: | Zeile 52: | ||
{| | {| | ||
|[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | ||
| − | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width=" | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="900" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Aufgabe_Drehung.ggb"/> |
</popup> | </popup> | ||
|} | |} | ||
Version vom 12. Juni 2010, 16:08 Uhr
Lernpfad-Navigator
Drehung
| Arbeitsauftrag
Die nächste Abbildung ist die Drehung mit verschiedenen Bereichen: beliebiger Drehwinkel, Drehpunkt, besondere Drehungen... Schaus dir an! |
{{#slideshare:drehung-100609155235-phpapp02}}
Das Geogebra Applet zeigt dir nochmal die Abbildung Drehung.
Leerzeile
Aufgabe
Es folgen nun eine Teilaufgabe aus einer ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigt, besonders mit der Drehung.
Die Punkte 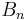 können auf die Punkte können auf die Punkte 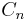 abgebildet werden. abgebildet werden.
Berechnen Sie die Koordinaten der Eckpunkte |
Leerzeile
Leerzeile
Weiter gehts zu Abbildung durch Achsenspiegelung
Leerzeile
Abbildungen im Koordinatensystem
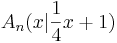 auf der Geraden g mit der Gleichung
auf der Geraden g mit der Gleichung 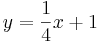 und Punkte
und Punkte 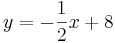 bilden zusammen mit den Punkten
bilden zusammen mit den Punkten 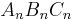 . Die Abzisse der Punkte
. Die Abzisse der Punkte 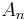 .
.