4.Station: Unterschied zwischen den Versionen
(Bild eingefügt) |
|||
| Zeile 5: | Zeile 5: | ||
==4. Station: Längenverhältnistreue== | ==4. Station: Längenverhältnistreue== | ||
| + | [[Bild:Porzelt_lobenderDia3.jpg]] | ||
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
[[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Längenverhältnistreue''' liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist. | [[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Längenverhältnistreue''' liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist. | ||
| Zeile 49: | Zeile 50: | ||
<math>{\overline{A'P'}\over\overline{P'B'}}</math> = '''<math>{1,4\ cm \over 3\ cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | <math>{\overline{A'P'}\over\overline{P'B'}}</math> = '''<math>{1,4\ cm \over 3\ cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | ||
</div> | </div> | ||
| − | + | <br> | |
| + | [[Bild:Porzelt_lobenderPanto6.jpg]] | ||
<br> | <br> | ||
Version vom 12. Juli 2009, 21:35 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
4. Station: Längenverhältnistreue
Längenverhältnistreue liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist.
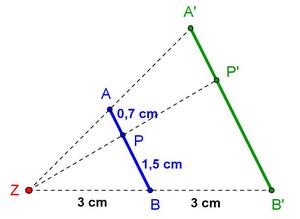 |
Arbeitsauftrag:
1.Berechne den Streckungsfaktor k. |
Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.
Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:
Lösung zu 1:
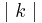 =
= 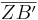 :
: 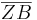
Einsetzen der Werte:
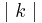 = 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)
= 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)
 |
Lösung zu 2: |
Lösung zu 3:
Einsetzen der Werte:
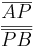 =
= 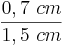 = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
= 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
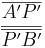 =
= 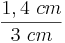 = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
= 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
Für 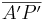 kann man auch
kann man auch 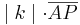 und für
und für 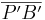 kann man
kann man 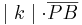 einsetzen.
einsetzen.
Daraus folgt: 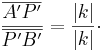
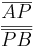 .
.
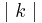 kann man rauskürzen, so dass
kann man rauskürzen, so dass 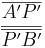
 gilt.
gilt.
Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)





 Weiter zur 5. Station
Weiter zur 5. Station Zurück zur 3. Station
Zurück zur 3. Station
