Wiederholung-2: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 67: | Zeile 67: | ||
|} | |} | ||
</div> | </div> | ||
| + | <ggb_applet height="600" width="750" showResetIcon="true" filename="KS_DreieckABC.ggb" /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | a) Verschiebe den Punkt C so, dass das Dreieck gleichschenklig ist. Wie lauten die x-Werte von C? ''-es gibt mehr als eine Lösung!-'' | ||
| + | (0) (-1) (!5) (!-2) (!-5) (!1) (!-7) (!2) (!3) (!-4) | ||
| + | |||
| + | b) Gib das Intervall für x an, so dass das Dreieck ABC spitzwinklig ist. | ||
| + | (![-5|2]) ([-5,3|3,3]) (![2,2|5,1]) (![-6|-2]) (![0|4,5]) (![-3,2|0]) | ||
| + | |||
| + | </div> | ||
| + | c) Zeige, dass es kein Dreieck ABC mit <math>\gamma</math> = 90° gibt. | ||
| + | <br /> | ||
| + | ''Hinweis: Überlege ob [AB] die längste Seite sein kann.'' | ||
| + | <br /> | ||
| + | <br /> | ||
[[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck/Seiten-Winkel-Beziehung|<math>\Rightarrow</math> Super! Jetzt geht es hier weiter!]] | [[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck/Seiten-Winkel-Beziehung|<math>\Rightarrow</math> Super! Jetzt geht es hier weiter!]] | ||
Version vom 26. Februar 2010, 19:37 Uhr
Je nach Größe der Winkel und Länge der Seiten kann ich verschiedene Formen annehmen. Kennst du sie noch alle?
Zuordnung
Ordne die Satzteile den Begriffen zu, so dass die richtigen Definitionen entstehen. Ziehe die grünen Felder dazu hinter das entsprechende graue Feld.
rechtwinkliges Dreieck:
stumpfwinkliges Dreieck:
gleichschenkliges Dreieck:
gleichseitiges Dreieck:
spitzwinkliges Dreieck:
(kleiner als) 90°(zwei Schenkel) sind gleich lang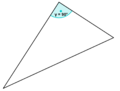
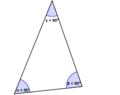alle drei Winkel sind gleich groß (60°)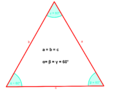
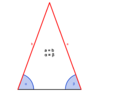(größer als) 90°
zwei Seitensind gleich langein Winkel beträgtein Winkel >genau 90°alle drei Winkel <alle drei Seiten
Wenn du die Satzteile richtig zugeordnet hast, klicke hier um die Definitionen anzuzeigen:
[Anzeigen]
Aufgabe
Übertrage die Definitionen auf deinen Laufzettel! |
Sehr schön! Jetzt haben wir die verschiedenen Formen gesehen und definiert. Findest du im memo-quiz die richtigen Paare mit Bild und Bezeichnung?
rechtwinkliges Dreieck
spitzwinkliges Dreieck gleichschenkliges Dreieck
stumpfwinkliges Dreieck
gleichseitiges Dreieck
Das war nicht so schwer. Findest du auch die richtigen Dreiersets mit Bezeichnung, Bild und Definition?
gleichschenkliges Dreieck Alle drei Winkel < (sind kleiner als) 90°.
stumpfwinkliges Dreieck Ein Winkel beträgt genau 90°.
rechtwinkliges Dreieck Zwei Seiten sind gleich lang.
Ein Winkel > (ist größer als) 90°.
Alle drei Seiten sind gleich lang und alle drei Winkel gleich groß (60°).
spitzwinkliges Dreieck gleichseitiges Dreieck
a) Verschiebe den Punkt C so, dass das Dreieck gleichschenklig ist. Wie lauten die x-Werte von C? -es gibt mehr als eine Lösung!-
b) Gib das Intervall für x an, so dass das Dreieck ABC spitzwinklig ist.
c) Zeige, dass es kein Dreieck ABC mit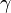 
= 90° gibt.
Hinweis: Überlege ob [AB] die längste Seite sein kann.
Super! Jetzt geht es hier weiter!
