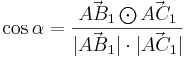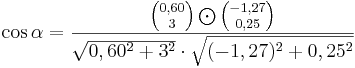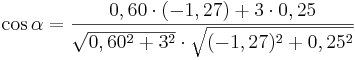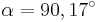Skalarprodukt: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
|||
| Zeile 29: | Zeile 29: | ||
<poem> | <poem> | ||
| − | |||
| − | |||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 36: | Zeile 34: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | Hier | + | Hier hast du es ebenfalls mit alten Abschlussprüfunen zu tun. Hier sind allerdings Vektoren in Abhängigkeit eines Winkels gegeben. Um Koordinaten oder Winkel zu berechenn solltest du das Skalarprodukt verwenden! |
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 ''' | + | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | + | Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; B2). | |
| + | ------------ | ||
| + | Die Pfeile <math>\vec{AB_n}={3 \cdot \cos \varphi -2 \choose 3}</math> und <math>\vec{AC_n}={2 \cdot \cos \varphi -3 \choose {\sin}^2 \varphi}</math> mit <math>\quad A(2|1)</math> spannen für <math>\varphi \in [0^\circ; 180^\circ]</math> Dreiecke <math>\quad AB_nC_n</math> auf. | ||
|} | |} | ||
| − | < | + | |
| − | {| | + | {| |
| − | | <math>\quad | + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] |
| − | | | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Gleichschenklig-Rechtwinklig.ggb"/> |
| − | | <math>\ | + | </popup> |
| − | + | |} | |
| − | + | ||
| − | + | {| border="1" | |
| − | + | |Für <math>\quad \varphi =30^\circ</math> ergeben sich die Vektoren <math>\quad \vec{AB_1}</math> und <math>\quad \vec{AC_n}</math>, die einen Winkel mit dem Maß <math>\quad \alpha</math> einschließen. Berechnen sie das Maß <math>\quad \alpha</math> auf 2 Stellen gerundet. | |
| + | <popup name="Lösung"> | ||
| + | [[Bild:Peter_Fischer_Formelsammlung.png|40px]] | ||
| + | * <math>\cos \alpha =\frac{\vec{AB_1} \bigodot \vec{AC_1}}{|\vec{AB_1}| \cdot |\vec{AC_1}|}</math> | ||
| + | * <math>\cos \alpha =\frac{{0,60 \choose 3} \bigodot {-1,27 \choose 0,25}}{\sqrt{0,60^2+3^2} \cdot \sqrt{(-1,27)^2+0,25^2}}</math> | ||
| + | * <math>\cos \alpha =\frac{0,60 \cdot (-1,27)+3 \cdot 0,25}{\sqrt{0,60^2+3^2} \cdot \sqrt{(-1,27)^2+0,25^2}}</math> | ||
| + | * <math>\alpha=90,17^\circ</math> | ||
| + | </popup> | ||
| + | |||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: <math>\quad \alpha</math>={ 90,17 _7}° (2 Nachkommastellen) | ||
| + | </quiz> | ||
|} | |} | ||
| − | |||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
{| border="1" | {| border="1" | ||
| − | + | |Die Punkte C<sub>n</sub> können in Abhängigkeit der Abszisse x der Punkte M<sub>n</sub> dargestellt werden als <math>\quad C_n(3x-6|-x+6)</math>. Ermittle die Gleichung des Trägergraphen h der Punkte C<sub>n</sub>. | |
| − | + | Das Ergebnis kannst du im Applet erkennen, wenn du auf "Trägergraph h einblenden" klickst. | |
| − | + | ||
| − | + | ||
|} | |} | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | {| border="1" | ||
| + | |Zeige, dass für den Flächeninhalt A der Dreiecke <math>\quad AB_nC</math> in Abhängigkeit von der Abzisse x der Punkte M<sub>n</sub> gilt: <math>\quad A(x)=85x^2-24x+36)</math>FE | ||
| + | <popup name="Tipp"> Suche einfache, flächengleiche Figuren!</popup> | ||
| + | |} | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | |||
| + | {| border="1" | ||
| + | |Die Dreiecke <math>\quad AB_3C_3</math> und <math>\quad AB_4C_4</math> haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C<sub>3</sub> und C<sub>4</sub>. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ | { | ||
| type="{}" } | | type="{}" } | ||
| − | + | Lösung: C<sub>3</sub>{ -6 _3}|{ 6 _3} und C<sub>4</sub>{ 8,4 _3}|{ 1,2 _3} (1 Nachkommastelle) | |
| − | + | </quiz> | |
| − | < | + | |} |
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
| − | < | + | |
| − | + | {| border="1" | |
| + | |Unter den Dreiecken AB<sub>n</sub>C<sub>n</sub> gibt es das Dreieck AB<sub>5</sub>C<sub>5</sub>, bei dem der Punkt C<sub>5</sub> auf der Geraden g liegt. | ||
| + | Ermitteln Sie die Koordinaten des Punktes C<sub>5</sub> und überlegen Sie sich, dass das Dreieck AB<sub>5</sub>C<sub>5</sub> den kleinsten Flächeninhalt aller Dreiecke AB<sub>n</sub>C<sub>n</sub> besitzt. | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: C<sub>5</sub>{ 1,2 _3}|{ 3,6 _3} (1 Nachkommastelle) | ||
</quiz> | </quiz> | ||
| + | |} | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
<poem> | <poem> | ||
'''Weiter gehts zu [[Trigonometrische Funktionen]]''' | '''Weiter gehts zu [[Trigonometrische Funktionen]]''' | ||
Version vom 6. Juni 2010, 12:13 Uhr
Trigonometrie
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! |
{{#slideshare:skalarprodukt-100603045003-phpapp01}}
Leerzeile
Aufgaben
Hier hast du es ebenfalls mit alten Abschlussprüfunen zu tun. Hier sind allerdings Vektoren in Abhängigkeit eines Winkels gegeben. Um Koordinaten oder Winkel zu berechenn solltest du das Skalarprodukt verwenden!
| Aufgabe 1 Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; B2). Die Pfeile |
Für 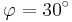 ergeben sich die Vektoren ergeben sich die Vektoren 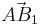 und und 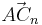 , die einen Winkel mit dem Maß , die einen Winkel mit dem Maß 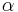 einschließen. Berechnen sie das Maß einschließen. Berechnen sie das Maß 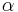 auf 2 Stellen gerundet. auf 2 Stellen gerundet.
|
Leerzeile
Die Punkte Cn können in Abhängigkeit der Abszisse x der Punkte Mn dargestellt werden als 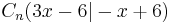 . Ermittle die Gleichung des Trägergraphen h der Punkte Cn. . Ermittle die Gleichung des Trägergraphen h der Punkte Cn.
Das Ergebnis kannst du im Applet erkennen, wenn du auf "Trägergraph h einblenden" klickst. |
Leerzeile
Zeige, dass für den Flächeninhalt A der Dreiecke 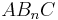 in Abhängigkeit von der Abzisse x der Punkte Mn gilt: in Abhängigkeit von der Abzisse x der Punkte Mn gilt: 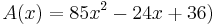 FE FE
|
Leerzeile
Die Dreiecke 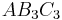 und und 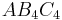 haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C3 und C4. haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C3 und C4.
|
Leerzeile
| Unter den Dreiecken ABnCn gibt es das Dreieck AB5C5, bei dem der Punkt C5 auf der Geraden g liegt.
Ermitteln Sie die Koordinaten des Punktes C5 und überlegen Sie sich, dass das Dreieck AB5C5 den kleinsten Flächeninhalt aller Dreiecke ABnCn besitzt. |
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
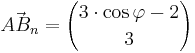 und
und 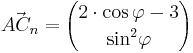 mit
mit 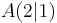 spannen für
spannen für ![\varphi \in [0^\circ; 180^\circ]](/images/math/3/f/f/3ffe9fc716cf41576effb3bafe19b7cc.png) Dreiecke
Dreiecke 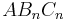 auf.
auf.