Abbildungen im Koordinatensystem: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
[[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude> | [[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude> | ||
| − | ==Abbildungen im Koordinatensystem== | + | ==Abbildungen im Koordinatensystem - Parallelverschiebung== |
{| border="0" | {| border="0" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| Zeile 30: | Zeile 30: | ||
<poem> | <poem> | ||
| − | <ggb_applet height="600" width="1000" showMenuBar=" | + | Das folgende GeoGebra-Applet zeigt dir zur Wiederholung eine Parallelverschiebung, deren Verschiebungsvektor du verändern kannst. |
| + | <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Parallelverschiebung.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
Version vom 10. Juni 2010, 17:55 Uhr
Abbildungen im Koordinatensystem - Parallelverschiebung
| Arbeitsauftrag
Hier geht es nicht um die Eigenschaften der Abbildungen, die solltest du schon eine Weile kennen und kannst sie auch in der Formelsammlung nachschlagen. Stattdesssen solltest du Bildpunkte mit Hilfe von Abbildungsmatrizen berechnen können. Die Rechnung mit Matrizen wird nochmal erklärt, anschließend wird die Parallelverschiebung als erste Abbildung verdeutlicht. |
{{#slideshare:parallelverschiebung-100609155245-phpapp01}}
Das folgende GeoGebra-Applet zeigt dir zur Wiederholung eine Parallelverschiebung, deren Verschiebungsvektor du verändern kannst.
Leerzeile
Aufgaben
Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!
| Aufgabe 1 Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. |
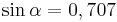 |
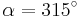 |
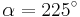
|
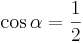 |
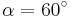 |
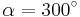
|
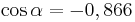 |
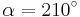 |
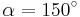
|
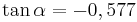 |
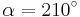 |
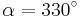
|
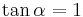 |
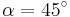 |
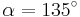
|
Leerzeile
| Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. |
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile

