Trigonometrie: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 13: | Zeile 13: | ||
**[[Exkurs: Figuren und ihre Eigenschaften]] | **[[Exkurs: Figuren und ihre Eigenschaften]] | ||
*[[Abbildungen im Koordinatensystem]] | *[[Abbildungen im Koordinatensystem]] | ||
| + | *[[Prüfungsaufgaben]] | ||
</div> | </div> | ||
<div style="font-size:90%; padding: .5em; background-color:#FFD700; border-top:1px solid #aaaaaa;"> | <div style="font-size:90%; padding: .5em; background-color:#FFD700; border-top:1px solid #aaaaaa;"> | ||
| Zeile 29: | Zeile 30: | ||
<poem> | <poem> | ||
| − | <ggb_applet height="600" width=" | + | <ggb_applet height="600" width="900" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Einheitskreis.ggb" /> |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 67: | Zeile 68: | ||
-------- | -------- | ||
Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. | Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. | ||
| + | |} | ||
| + | |||
| + | <math>\quad {\sin}^2 \alpha +2 cos \alpha =0,5</math> | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | <math>\quad {\sin}^2 \alpha </math> durch <math>\quad 1-{\cos}^2 \alpha</math> ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen. | ||
| + | </popup> | ||
|} | |} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ | { | ||
| type="{}" } | | type="{}" } | ||
| − | + | '''Lösung:''' <math>\quad \alpha_1</math>={ 73,14 _7}; <math>\quad \alpha_2</math>={ 286,86 _7} (2 Nachkommastellen) | |
| − | + | </quiz> | |
| − | Lösung: <math>\quad \alpha_1</math>={ 73,14 _7}; <math>\quad \alpha_2</math>={ 286,86 _7} (2 Nachkommastellen) | + | |
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
<math>\quad \sin \alpha=\sqrt{3} \cdot \cos \alpha</math> | <math>\quad \sin \alpha=\sqrt{3} \cdot \cos \alpha</math> | ||
| − | <popup name="Tipp"> <math>\frac{\sin \alpha}{\cos \alpha}=\tan \alpha</math> | + | {| |
| − | Lösung: <math>\quad \alpha_1</math>={ 60,00 _7}; <math>\quad \alpha_2</math>={ 240,00 _7} | + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] |
| + | |<popup name="Tipp"> | ||
| + | <math>\frac{\sin \alpha}{\cos \alpha}=\tan \alpha</math> | ||
| + | </popup> | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | '''Lösung:''' <math>\quad \alpha_1</math>={ 60,00 _7}; <math>\quad \alpha_2</math>={ 240,00 _7} | ||
</quiz> | </quiz> | ||
Version vom 12. Juni 2010, 15:32 Uhr
Lernpfad-Navigator
Trigonometrie
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! |
{{#slideshare:sinuskosinustangens-100609154155-phpapp01}}
Leerzeile
Aufgaben
Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!
| Aufgabe 1 Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. |
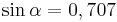 |
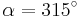 |
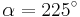
|
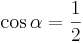 |
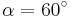 |
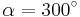
|
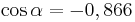 |
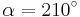 |
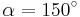
|
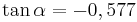 |
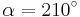 |
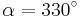
|
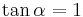 |
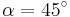 |
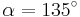
|
Leerzeile
| Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. |
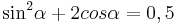
Leerzeile
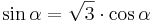
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
Trigonometrie
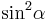 durch
durch 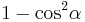 ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.
ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.