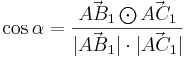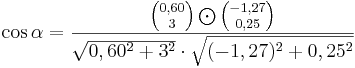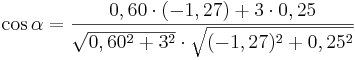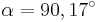Exkurs Geometrie: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
|||
| Zeile 20: | Zeile 20: | ||
[[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude> | [[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude> | ||
| − | ==Wichtiges zur Geometrie== | + | |
| + | == Wichtiges zur Geometrie == | ||
| + | |||
{| border="0" | {| border="0" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| Zeile 26: | Zeile 28: | ||
-------- | -------- | ||
Auf dieser Seite sollen nocheinmal Themen zur Geometrie wiederholt werden, die bereits vor der zehnten Klasse bekannt sein sollen und für die Prüfung wichtig sein können|} | Auf dieser Seite sollen nocheinmal Themen zur Geometrie wiederholt werden, die bereits vor der zehnten Klasse bekannt sein sollen und für die Prüfung wichtig sein können|} | ||
| + | |} | ||
| + | |||
| + | <poem> | ||
| + | |||
| + | === Flächeninhaltsberechnungen === | ||
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width="1000" style="text-align:left" style="background-color:#FFEC8B;" | + | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"|'''Generelles um Flächeninhalte von Figuren zu ermitteln. [[Bild:Peter_Fischer_Idee.png|40px]] ''' |
| − | | | + | ---------------------- |
| − | -------- | + | *Flächenformeln |
| − | + | *Flächenberechnung durch Zerlegung | |
| + | *Flächeninhalt von Dreiecken | ||
|} | |} | ||
| + | |||
| + | ==== '''Flächenformeln''' ==== | ||
| + | Im laufe deiner Schulzeit hast du für verschiedene Figuren Flächenformeln kennengelernt, wie <math>\quad a^2</math> für das Quadrat, <math>\quad a \cdot b</math> für der Rechteck oder <math>\quad g \cdot h</math> für das Parallelogramm. Eine Übersicht dieser Formeln findest du auf dem MindMap ''"Figuren und ihre Eigenschaften"''. Wenn du alle Angaben hast, um diese Formeln zu benutzen ist alles gut. | ||
| + | |||
| + | |||
| + | ==== '''Flächenberechnung durch Zerlegung''' ==== | ||
| + | Falls dir Angaben fehlen oder es keine Formel für diese Figur existiert, so kannst du versuchen sie in einfachere Figuren zu Zerlegen. Häufig hilft es Figuren in Dreiecke zu zerlegen, da für Dreiecke mehrere Formeln zur Verfügung stehen. | ||
| + | ==== '''Flächeninhalt von Dreiecken''' ==== | ||
Version vom 15. Juni 2010, 11:21 Uhr
Wichtiges zur Geometrie
| Bemerkung
Auf dieser Seite sollen nocheinmal Themen zur Geometrie wiederholt werden, die bereits vor der zehnten Klasse bekannt sein sollen und für die Prüfung wichtig sein können|} |
=== Flächeninhaltsberechnungen ===
Generelles um Flächeninhalte von Figuren zu ermitteln.
|
==== Flächenformeln ====
Im laufe deiner Schulzeit hast du für verschiedene Figuren Flächenformeln kennengelernt, wie 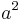 für das Quadrat,
für das Quadrat, 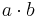 für der Rechteck oder
für der Rechteck oder 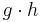 für das Parallelogramm. Eine Übersicht dieser Formeln findest du auf dem MindMap "Figuren und ihre Eigenschaften". Wenn du alle Angaben hast, um diese Formeln zu benutzen ist alles gut.
für das Parallelogramm. Eine Übersicht dieser Formeln findest du auf dem MindMap "Figuren und ihre Eigenschaften". Wenn du alle Angaben hast, um diese Formeln zu benutzen ist alles gut.
==== Flächenberechnung durch Zerlegung ====
Falls dir Angaben fehlen oder es keine Formel für diese Figur existiert, so kannst du versuchen sie in einfachere Figuren zu Zerlegen. Häufig hilft es Figuren in Dreiecke zu zerlegen, da für Dreiecke mehrere Formeln zur Verfügung stehen.
==== Flächeninhalt von Dreiecken ====
{{#slideshare:skalarprodukt-100609154205-phpapp01}}
Leerzeile
Aufgaben
Hier hast du es ebenfalls mit alten Abschlussprüfunen zu tun. Hier sind allerdings Vektoren in Abhängigkeit eines Winkels gegeben. Um Koordinaten oder Winkel zu berechenn solltest du das Skalarprodukt verwenden!
| Aufgabe 1 Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; B2). Die Pfeile |
Für 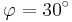 ergeben sich die Vektoren ergeben sich die Vektoren 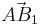 und und 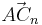 , die einen Winkel mit dem Maß , die einen Winkel mit dem Maß 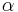 einschließen. Berechnen sie das Maß einschließen. Berechnen sie das Maß 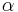 auf 2 Stellen gerundet. auf 2 Stellen gerundet.
|
Leerzeile
Berechnen Sie den Wert von 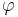 , sodass der Punkt C4 auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C4. ( , sodass der Punkt C4 auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C4. (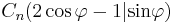 ) )
|
Leerzeile
Im rechtwinkligen Dreieck A5C5 ist die Strecke [B5C5] die Hypothenuse. Berechnen Sie den zugehörigen Wert von 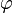 . .
|
Leerzeile
Weiter gehts zu Abschnitt IV Abbildungen im Koordinatensystem
Leerzeile
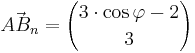 und
und 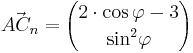 mit
mit 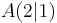 spannen für
spannen für ![\varphi \in [0^\circ; 180^\circ]](/images/math/3/f/f/3ffe9fc716cf41576effb3bafe19b7cc.png) Dreiecke
Dreiecke 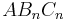 auf.
auf.