4.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(fragender Dia eingefügt) |
(Formel bearbeitet) |
||
| Zeile 59: | Zeile 59: | ||
</div> | </div> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Für <math>\overline{AP}</math> kann man auch ''' | + | Für <math>\overline{AP}</math> kann man auch '''<math>\mid k\mid \cdot \overline{A'P'}</math>''' und für <math>\overline{PB}</math> kann man '''<math>\mid k\mid \cdot \overline{P'B'}</math>''' einsetzen. <br> |
| − | Daraus folgt: <math>{\overline{AP}\over\overline{PB}} | + | Daraus folgt: <math>{\overline{AP}\over\overline{PB}} ={{|k|}\over{|k|}}\cdot</math> '''<math>{\overline{A'P'}\over\overline{P'B'}}</math>'''.<br> |
| − | + | <math>\mid k\mid</math> kann man rauskürzen, so dass '''<math>{\overline{AP}\over\overline{PB}}</math>''' <math>= {\overline{A'P'}\over\overline{P'B'}}</math> gilt. | |
</div> | </div> | ||
<br> | <br> | ||
Version vom 7. Juli 2009, 18:59 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
4. Station: Längenverhältnistreue
Längenverhältnistreue liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist.
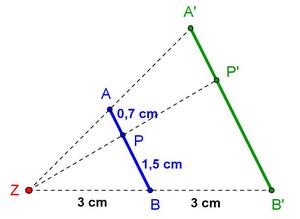 |
Arbeitsauftrag:
1.Berechne den Streckungsfaktor k. |
- Um herauszufinden ob deine Lösungen richtig sind, klicke hier die Lösung an:
Für 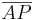 kann man auch
kann man auch 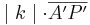 und für
und für 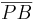 kann man
kann man 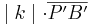 einsetzen.
einsetzen.
Daraus folgt: 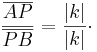
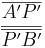 .
.
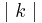 kann man rauskürzen, so dass
kann man rauskürzen, so dass 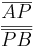
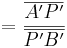 gilt.
gilt.
Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)

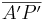 und
und 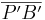 .
.


