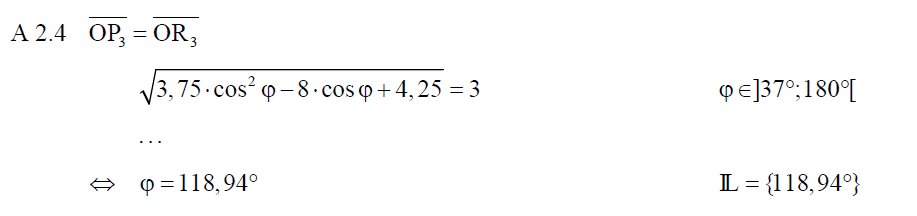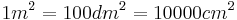Abschlussprüfung 2009A: Unterschied zwischen den Versionen
| Zeile 74: | Zeile 74: | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
|<popup name="Tipp"> | |<popup name="Tipp"> | ||
| − | Bilde Verhältnisse von <math>\quad r=[AD] </math> und <math>r'</math>, neuer Radius. | + | Bilde Verhältnisse von <math>\quad r=[AD] </math> und <math>r' \quad</math>, neuer Radius. |
</popup> | </popup> | ||
|} | |} | ||
Version vom 4. August 2010, 19:56 Uhr
Abschlussprüfung 2009 - Aufgabe A
Leerzeile
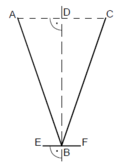
| A 1.1 Berechnen Sie das Maß des Winkels CBA. Runden Sie auf Ganze.
[Teilergebnis:
|
Leerzeile
| A 1.2 Berechnen Sie auf Millimeter gerundet, bis zu welcher Höhe der Messbecher gefüllt ist, wenn er einen halben Liter Flüssigkeit enthält.
|
Leerzeile
| Aufgabe A | |
| A 2.0 |
Leerzeile
A 2.2 Zeigen Sie rechnerisch, dass für die Länge der Strecken ![\quad [OP_n]](/images/math/a/5/0/a5096f64564da61dc54e186bf807d07a.png) in Abhängigkeit von in Abhängigkeit von 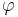 gilt: gilt:
|
Leerzeile
A 2.3 Begründen Sie, dass die Punkte 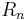 auf einer Kreislinie um Mittelpunkt O mit dem Radius auf einer Kreislinie um Mittelpunkt O mit dem Radius 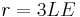 liegen. liegen.
|
A 2.4 Das Parallelogramm 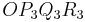 ist eine Raute. Diese wird durch die Pfeile ist eine Raute. Diese wird durch die Pfeile 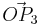 und und 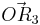 aufgespannt. aufgespannt.
Berechnen Sie das zugehörige Winkelmaß
|
| Aufgabe A | |
| A 3.0 |
| A 3.1 Berechnen Sie, wie groß der Inhalt der von Schimmelpilz befallenen Fläche bei der Platte A am Ende des 6. Versuchstages war. Runden Sie auf Quadratzentimeter.
Leerzeile
|
Leerzeile
| A 3.2 Bei der Platte A war der Versuch abgebrochen worden, als der Inhalt der von Schimmelpilz befallenen Fläche einen Quadratmeter erreicht hatte.
Ermitteln sie rechnerisch, am wie vielten Tag dies der Fall war. Leerzeile
|
Leerzeile
| A 3.3 Auch bei der Platte B hatte sich der Inhalt der vom Schimmelpilz befallenen Fläche täglich um einen festen Prozentsatz vergrößert. Hier war
ein Quadratmeter am Ende des 13. Versuchstages erreicht worden. Berechnen Sie den Prozentsatz.
|
Leerzeile
Weiter gehts zu Abschlussprüfung 2009 - Aufgabe B
Leerzeile
 ist die Symmetrieachse.
ist die Symmetrieachse. .
.
 ]
]
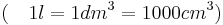

![\quad r=[AD]](/images/math/9/b/3/9b390cbd39ab6fa16a8b76d657a5d735.png) und
und 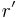 , neuer Radius.
, neuer Radius.

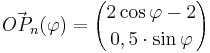 und
und 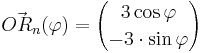 mit
mit 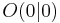 spannen für
spannen für ![\quad \varphi \in ]37^\circ;180^\circ[](/images/math/5/4/d/54d0df6d5a6a766caacaeadfb04fc212.png) Parallelogramme
Parallelogramme 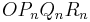 auf.
auf.
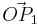 und
und 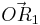 für
für 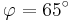 , sowie
, sowie 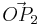 und
und 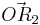 für
für 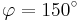 .
.
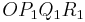 und
und 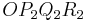 in ein Koordinatensystem ein.
in ein Koordinatensystem ein.

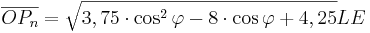
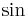 und
und 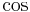 .
.