7.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(1. Aufgabe gelöscht) |
|||
| Zeile 5: | Zeile 5: | ||
==7. Station: Übung== | ==7. Station: Übung== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | ||
:Gegeben ist eine Gerade g, die durch den Punkt A(1|2) geht und die Steigung m= 0.5 besitzt. | :Gegeben ist eine Gerade g, die durch den Punkt A(1|2) geht und die Steigung m= 0.5 besitzt. | ||
Version vom 9. Juli 2009, 13:27 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
7. Station: Übung
- Gegeben ist eine Gerade g, die durch den Punkt A(1|2) geht und die Steigung m= 0.5 besitzt.
- a)Bestimme die Geradengleichung und zeichne die Gerade in ein Koordinatensystem ein.
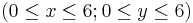
- b)Die Gerade g wird zentrisch mit Z(0|0) und k = 2 gestreckt. Konstruiere die Bildgerade g'.
- c)Berechne die Gleichung von g' mit Hilfe der zentrischen Streckung!
- Hake die richtige Lösung ab:
- Hier kannst du deine zeichnerische Lösung mit der von Dia vergleichen: