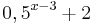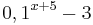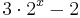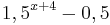Logarithmus
Aus DMUW-Wiki
< Lernpfade | Prüfungsvorbereitung | Exponential- und Logarithmusfunktion
Version vom 29. Mai 2010, 13:40 Uhr von Peter Fischer (Diskussion | Beiträge)
Lernpfad-Navigator
Logarithmus
| Arbeitsauftrag
Der Logarithmus hat für uns zwei Bedeutungen:
Auf den folgenden Folien wirst du an beide Aspekte erinnert. |
{{#slideshare:logarithmusfunktion-100529024425-phpapp02}}
Aufgaben
Die folgenden Aufgaben beziehen sich auf Exponentialgleichungen, x-Wertberechnungen von Exponentialfunktionen, da dies für deine Prüfung sehr relevant ist.
| Aufgabe 1
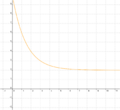
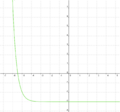
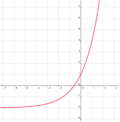
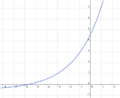
Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's! |
| Aufgabe 3 Berechnungen zu Exponentialfunktionen. |
Weiter gehts zu Logarithmus
Potenzen und Potenzfunktionen