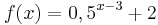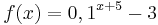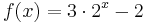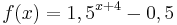Skalarprodukt

Lernpfad-Navigator

• Potenzen und Potenzfunktionen
• Exponential- & Logarithmusfunktion
• Trigonometrie
  • Trigonometrische Funktionen
  • Berechnungen in Dreiecken
  • Skalarprodukt
  • Exkurs: Figuren und ihre Eigenschaften
• Abbildungen im Koordinatensystem

LERNPFAD

Trigonometrie

	Arbeitsauftrag Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch!

{{#slideshare:skalarprodukt-100603045003-phpapp01}}

Leerzeile

Aufgaben

Hier warten nun Aufgaben zu Exponentialfunktionen, diese sind auch sehr häufig in der Abschlussprüfugn zu finden!

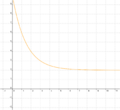
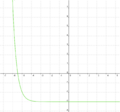
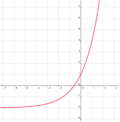
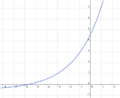
	Aufgabe 1 Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's!

$\quad f(x) = 0,5^{x-3}+2$
$\quad f(x) = 0,1^{x+5}-3$
$\quad f(x) = 3 \cdot 2^x-2$
$\quad f(x) = 1,5^{x+4}-0,5$

Leerzeile

	Aufgabe 2 Berechnungen zu Exponentialfunktionen.

1.

Die Gleichung $f_1: y=7-7 \cdot 2,72^{-0,5x}$ beschreibt welche Spannung y nach x Sekunden an einem Kondensator anliegt. Die maximale Spannung (Sättigungsspannung) ist 7V. Wie viel Prozent der Sättigungsspannung hat der Kondensator nach 2,60s erreicht? (Abschlussprüfung 2004; Aufgabengruppe A; 1.2)

Lösung:%

Tipp anzeigen Tipp verstecken Die Zeit in die Gleichung einsetzen und y ausrechnen. Anschließend in Prozent umrechnen.

Karl der Große (742-814) wurde im Jahr 800 römischer Kaiser. Angenommen er hätte in diesem Jahr einen Cent für dich angelegt auf einem Sparbuch. Du bekommst jährlich 2% Zins, der Zinsertrag bleibt auf dem Sparbuch. Wie viel Geld hättest du im Jahr 2010?

Tipp anzeigen Tipp verstecken Benutze die Zineszinsformel $K=K_0 \cdot (1+\frac{p}{100})^n$

Lösung: Mio. € (Auf ganze Milionen gerundet)

Punkte: 0 / 0

Weiter gehts zu Trigonometrische Funktionen
Leerzeile

Potenzen und Potenzfunktionen

LERNPFAD | Trigonometrie | Trigonometrische Funktionen | Berechnungen in Dreiecken | Skalarprodukt | Exkurs: Figuren und ihre Eigenschaften