4.Station
Aus DMUW-Wiki
< Lernpfade | Zentrische Streckung | Eigenschaften der zentrischen Streckung
Version vom 3. Juli 2009, 17:53 Uhr von Leonie Porzelt (Diskussion | Beiträge)
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
4. Station: Längenverhältnistreue
- Längenverhältnistreue liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist.
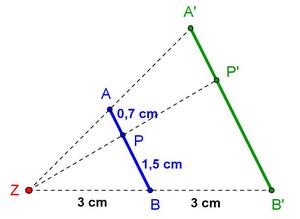 |
Arbeitsauftrag:
1.Berechne den Streckungsfaktor k. |
- Um herauszufinden ob deine Lösungen richtig sind, klicke hier die Lösung an:
- Warum ist
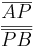 =
= 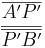 ?
?
Für 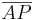 kann man auch |k| ∙
kann man auch |k| ∙ 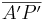 und für
und für 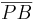 kann man |k| ∙
kann man |k| ∙ 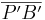 einsetzen.
einsetzen.
Daraus folgt: 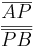 =
= 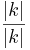 ∙
∙ 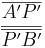 .
|k| kann man rauskürzen, so dass
.
|k| kann man rauskürzen, so dass 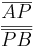 =
= 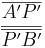 gilt.
gilt.
Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)

