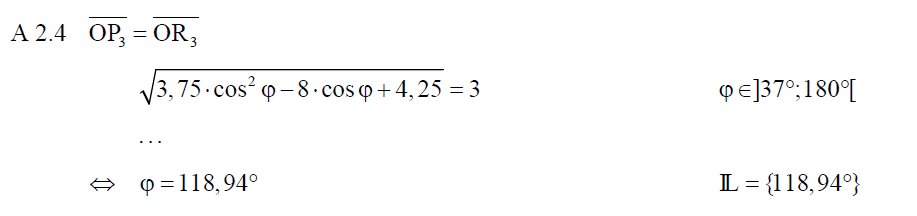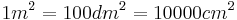Abschlussprüfung 2009B
Abschlussprüfung 2009 - Aufgabe B
| Aufgabe B | |
| B 1.0 |
Leerzeile
| B 1.1 Geben Sie die Definitionsmenge und Wertemenge der Funktion f sowie die Gleichung der Asymptote h an. | 
| ||
|
| |||
Leerzeile
Leerzeile
A 1.3 Punkte 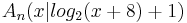 auf dem Graphen zu f sind zusammen mit dem Punkt auf dem Graphen zu f sind zusammen mit dem Punkt 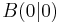 und den Punkten und den Punkten 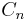 und und 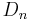 die Eckpunkte von Quadraten die Eckpunkte von Quadraten 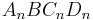 . .
Zeichnen Sie die Quadrate |
Leerzeile
B 1.4 Die Punkte 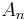 können auf die Punkte können auf die Punkte 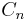 abgebildet werden. abgebildet werden.
Zeigen Sie durch Rechnung , dass der Trägergraph t der Punkte |
Leerzeile
B 1.5 Für das Quadrat 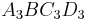 gilt: gilt: 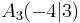 . .
Berechnen Sie die Koordinaten des Punktes
|
Leerzeile
B 1.6 Für das Quadrat 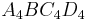 gilt: Der Punkt gilt: Der Punkt 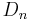 liegt auf der Winkelhalbierenden des II. Quadranten. liegt auf der Winkelhalbierenden des II. Quadranten.
Ermitteln Sie rechnersich die x-Koordinate des Punktes
|
| Aufgabe A | ||
| A 1.0 |
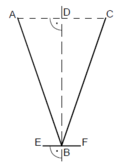
| |
A 2.1 Berechnen Sie die Koordinaten der Pfeile 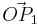 und und 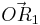 für für 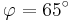 , sowie , sowie 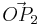 und und 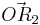 für für 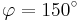 . Runden Sie auf zwei Stellen nach dem Komma. . Runden Sie auf zwei Stellen nach dem Komma.
Zeichnen Sie sodann die Parallelogramme Leerzeile
|
Leerzeile
A 2.2 Zeigen Sie rechnerisch, dass für die Länge der Strecken ![\quad [OP_n]](/images/math/a/5/0/a5096f64564da61dc54e186bf807d07a.png) in Abhängigkeit von in Abhängigkeit von 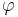 gilt: gilt:
|
Leerzeile
A 2.3 Begründen Sie, dass die Punkte 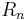 auf einer Kreislinie um Mittelpunkt O mit dem Radius auf einer Kreislinie um Mittelpunkt O mit dem Radius 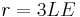 liegen. liegen.
|
A 2.4 Das Parallelogramm 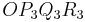 ist eine Raute. Diese wird durch die Pfeile ist eine Raute. Diese wird durch die Pfeile 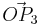 und und 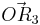 aufgespannt. aufgespannt.
Berechnen Sie das zugehörige Winkelmaß
|
| Aufgabe A | |
| A 3.0 |
| A 3.1 Berechnen Sie, wie groß der Inhalt der von Schimmelpilz befallenen Fläche bei der Platte A am Ende des 6. Versuchstages war. Runden Sie auf Quadratzentimeter.
Leerzeile
|
Leerzeile
| A 3.2 Bei der Platte A war der Versuch abgebrochen worden, als der Inhalt der von Schimmelpilz befallenen Fläche einen Quadratmeter erreicht hatte.
Ermitteln sie rechnerisch, am wie vielten Tag dies der Fall war. Leerzeile
|
Leerzeile
| A 3.3 Auch bei der Platte B hatte sich der Inhalt der vom Schimmelpilz befallenen Fläche täglich um einen festen Prozentsatz vergrößert. hier war ein Quadratmeter am Ende des 13. Versuchstages erreicht worden.
Berechnen Sie den Prozentsatz.
|
Leerzeile
Weiter gehts zu Abschlussprüfung 2009 - Aufgabe B
Leerzeile
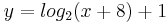 .
.
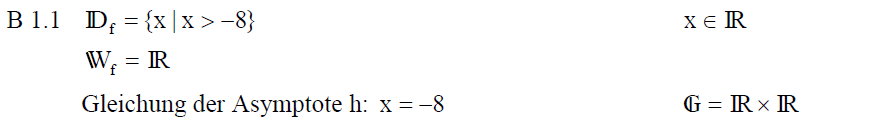
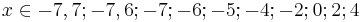 auf zwei Stellen nach dem Komma gerundet.
auf zwei Stellen nach dem Komma gerundet.
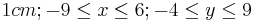


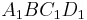 für
für 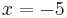 und
und 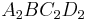 für
für 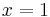 in das Koordinatensystem zu 1.2 ein.
in das Koordinatensystem zu 1.2 ein.
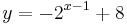 besitzt.
Zeichnen Sie den Trägergraphen t der Punkte
besitzt.
Zeichnen Sie den Trägergraphen t der Punkte 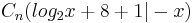 ]
]

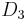 .
.

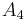
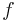 und
und 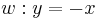 !
!

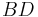 ist die Symmetrieachse.
ist die Symmetrieachse.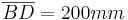 .
.
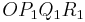 und
und 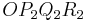 in ein Koordinatensystem ein.
in ein Koordinatensystem ein.

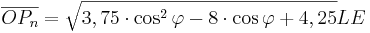
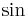 und
und 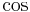 .
.