Ergänzungsgleichheit von Figuren

Ergänzungsgleichheit von Figuren

Du hast nun das Prinzip der Zerlegungsgleichheit kennen gelernt. Hier lernst Du noch eine weitere Eigenschaft der Zerlegungsgleichheit

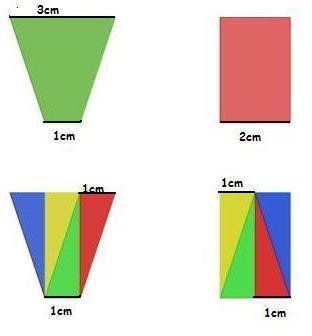
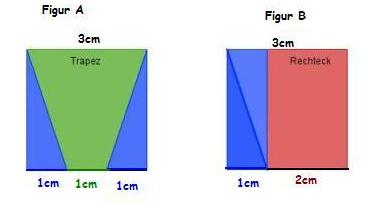
Das Trapez und das Rechteck sind zerlegungsgleich, denn sie können z.B. in jeweils vier zueinander kongruente Dreiecke zerlegt werden. Betrachte Dir dazu das nachfolgende Bild:

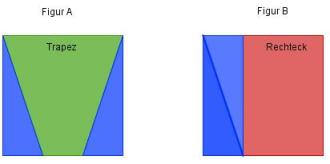
Man nennt dieses Rechteck und das Trapez aber auch ergänzungsgleich Betrachte Dir dazu das nachfolgende Bild:

Was bedeutet Ergänzungsgleichheit? Fülle dazu die Lücken aus:

Das                     und das Rechteck sind                     , das sie durch Ergänzung mit                     , in diesem Fall mit je                     blauen Dreiecken in zueinander kongruente Figuren                     überführt werden können.

zweiTrapezergänzungsgleichA und Bkongruenten Teilfiguren

Merke Dir folgende Definition zur Ergänzungsgleichheit gut und übetrage sie in Dein Heft!

Zwei Figuren sind ergänzungsgleich, wenn man sie durch Ergänzung mit kongruenten Teilfiguren in zerlegungsgleiche Figuren umwandeln kann. Ergänzungsgleiche Figuren sind daher auch zerlegungsgleich. Ergänzungsgleiche Figuren besitzen den gleichen Flächeninhalt.

Hier geht es zurück zur Seite
Zerlegungsgleichheit von Figuren
Hier geht es weiter zur Übung
Übung