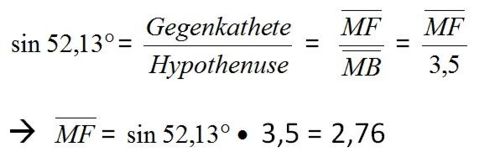Lösungsansatz: Unterschied zwischen den Versionen

Version vom 22. Juli 2010, 20:20 Uhr

Aufgabe: Berechne die Mantelfläche

Die Mantelfläche setzt sich aus den Dreiecken zusammen, die die Grundkanten
jeweils mit der Spitze S einschließen.
Um die Dreiecksflächen berechnen zu können, benötigst du die Dreieckshöhen.

In diesem Lösungsansatz erfährst du, wie man die Höhe des Dreiecks BCS errechnen kann:

1. Zunächst legst du den letzten Schalter (blau) oben im Applet um, um das nötige Stützdreieck MFS anzuzeigen.

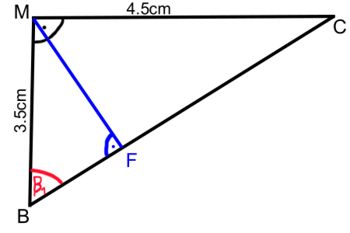
2. Als nächstes betrachten wir das Dreieck BCM:

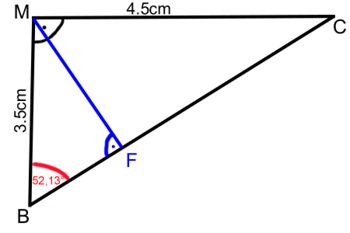
Nun berechnest du den Winkel im rechtwinkligen Dreieck BCM wiefolgt:

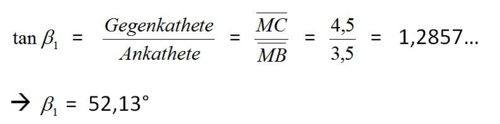
3. Nun berechnest du die Höhe des Dreiecks BCM. Dazu betrachten wir das Teildreieck BFM genauer:

Die Hypothenuse = 3,5cm ist gegeben und die Seite MF ist die Gegenkathete zum Winkel , also rechnest du MF wiefolgt:

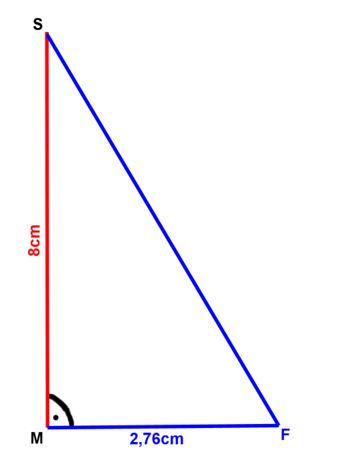
4. Nun wird letzlich noch das eingeblendete Stützdreieck MFS genauer betrachtet:

In diesem rechtwinkligen Dreieck entspricht die Hypothenuse der gesuchten Dreieckshöhe .
Mit Hilfe des Satz des Pythagoras sieht die Rechnung folgendermaßen aus:

Damit lässt sich nun die Fläche des Dreiecks BCS berechnen.
Gehe nun zurück. Fahre nun analog selbständig mit der Berechnung der Mantelfläche fort!