Berechnungen in Dreiecken: Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
{| border="1" | {| border="1" | ||
| − | |Berechne den Winkel <math>\quad ADM_2</math>, wobei D der Schnittpunkt von g und AC<sub>2</sub> ist. Der Punkt C<sub>2</sub> besitzt die Koordinaten <math>\quad C_2(3|3)</math>. | + | |Berechne den Winkel <math>\quad \angle ADM_2</math>, wobei D der Schnittpunkt von g und AC<sub>2</sub> ist. Der Punkt C<sub>2</sub> besitzt die Koordinaten <math>\quad C_2(3|3)</math>. |
{| | {| | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| Zeile 65: | Zeile 65: | ||
*<math>\quad \overline {AD}</math> und <math>\quad \overline {DM_2}</math> mit der Formel für Streckenlänge ermitteln | *<math>\quad \overline {AD}</math> und <math>\quad \overline {DM_2}</math> mit der Formel für Streckenlänge ermitteln | ||
*Kosinussatz im Dreieck <math>AM_2D \quad</math> anwenden | *Kosinussatz im Dreieck <math>AM_2D \quad</math> anwenden | ||
| − | *Alternativ kann auch die Innenwinkelsumme verwendet werden, wenn Winkel | + | *Alternativ kann auch die Innenwinkelsumme verwendet werden, wenn Winkel <math>\quad \angle DM_2A</math> mit <math>\quad \tan \alpha =m_g</math> berechnet wird. |
</popup> | </popup> | ||
|} | |} | ||
| Zeile 71: | Zeile 71: | ||
{ | { | ||
| type="{}" } | | type="{}" } | ||
| − | '''Lösung:''' <math>\quad \ | + | '''Lösung:''' <math>\quad \angle ADM_2</math>={ 71.57 _7}° (2 Nachkommastellen) |
</quiz> | </quiz> | ||
|} | |} | ||
| Zeile 86: | Zeile 86: | ||
{| border="1" | {| border="1" | ||
| − | |Zeige, dass für den Flächeninhalt A der Dreiecke <math>\quad AB_nC</math> in Abhängigkeit von der Abzisse x der Punkte M<sub>n</sub> gilt: <math>\quad A(x)=85x^2-24x+36)</math>FE | + | |Zeige, dass für den Flächeninhalt A der Dreiecke <math>\quad AB_nC</math> in Abhängigkeit von der Abzisse x der Punkte M<sub>n</sub> gilt: <math>\quad A(x)=(85x^2-24x+36)</math>FE |
{| | {| | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
Version vom 21. Juli 2010, 10:57 Uhr
Trigonometrie
| Arbeitsauftrag
Die wichtigeste Anwendung von Sinus, Cosinus und Tangens sind Berechnungen an Dreiecken, um Längen und Winkel zu ermitteln. Es gibt Sätze zur Brechnung an
Mit ihrer Hilfe lassen sich fast alle Längen berechnen, denn alle Figuren und auch Körper lassen in Dreiecke zerlegen! |
{{#slideshare:dreiecke-100609154147-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Berechnungen in Dreiecken
Berechnungen in Dreiecken
Leerzeile
Aufgaben
Nun kommen ein paar Aufgabn aus ehemaligen Abschlussprüfungen zu funktionaler Abhängigkeit und Berechnungen in Dreiecken.
Berechne den Winkel 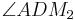 , wobei D der Schnittpunkt von g und AC2 ist. Der Punkt C2 besitzt die Koordinaten , wobei D der Schnittpunkt von g und AC2 ist. Der Punkt C2 besitzt die Koordinaten 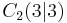 . .
|
Leerzeile
Die Punkte Cn können in Abhängigkeit der Abszisse x der Punkte Mn dargestellt werden als 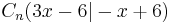 . Ermittle die Gleichung des . Ermittle die Gleichung des
Trägergraphen h der Punkte Cn. Das Ergebnis siehst du im Applet, wenn du x veränderst, die Punkte Cn zeichnen den Trägergraphen. |
Leerzeile
Zeige, dass für den Flächeninhalt A der Dreiecke 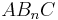 in Abhängigkeit von der Abzisse x der Punkte Mn gilt: in Abhängigkeit von der Abzisse x der Punkte Mn gilt: 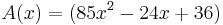 FE FE
|
Leerzeile
Die Dreiecke 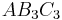 und und 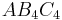 haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C3 und C4. haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C3 und C4.
|
Leerzeile
| Unter den Dreiecken ABnCn gibt es das Dreieck AB5C5, bei dem der Punkt C5 auf der Geraden g liegt.
Ermitteln Sie die Koordinaten des Punktes C5 und überlegen Sie sich, dass das Dreieck AB5C5 den kleinsten Flächeninhalt aller Dreiecke ABnCn besitzt. |
Leerzeile
Berechnen sie das größmögliche Maß  . .
|
Leerzeile
Zeigen Sie, dass für die Streckenlänge 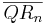 in Abhängigkeit von in Abhängigkeit von 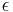 gilt: gilt:
|
Leerzeile
Berechnen Sie das Winkelmaß 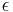 so, dass die Strecke so, dass die Strecke ![\quad [QR_1]](/images/math/1/b/f/1bff42e8e7c8dc3254891d165380ddf3.png) und und ![\quad [QS]](/images/math/6/8/1/681d454076a98ce0d45cfe29848e28ea.png) gleich land sind. gleich land sind.
|
Weiter gehts zu Skalarprodukt
Leerzeile
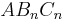 bilden eine Dreiecksschar mit dem gemeinsamen Punkt
bilden eine Dreiecksschar mit dem gemeinsamen Punkt 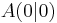 . Auf der Geraden g mit der Gleichung
. Auf der Geraden g mit der Gleichung 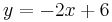 liegen die Mittelpunkte
liegen die Mittelpunkte 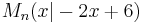 der Hyptenusen
der Hyptenusen ![\quad[AB_n]](/images/math/7/8/9/7897709debcde617572554254fb5973c.png) .
.
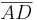 und
und 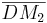 mit der Formel für Streckenlänge ermitteln
mit der Formel für Streckenlänge ermitteln
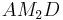 anwenden
anwenden
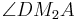 mit
mit 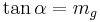 berechnet wird.
berechnet wird.
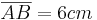 ist die Grundfläche einer PyramideABCDS. Die Spitze S liegt senkrecht über dem Eckpunkt A. Der Winkel SCA hat das Maß
ist die Grundfläche einer PyramideABCDS. Die Spitze S liegt senkrecht über dem Eckpunkt A. Der Winkel SCA hat das Maß 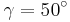 .
Der Punkt liegt auf der Kante
.
Der Punkt liegt auf der Kante ![\quad[AS]](/images/math/1/b/1/1b1864eaf7f103073ea35300bdc9b2cc.png) mit
mit 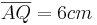 . Die Punkte
. Die Punkte 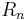 liegenauf der Kante
liegenauf der Kante ![\quad [CS]](/images/math/5/e/7/5e7a3de0416f94a037269c8c4f5914b7.png) , wobei die Winkel
, wobei die Winkel 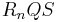 das Maß
das Maß  haben.
haben.
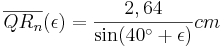 .
[Teilergebnis:
.
[Teilergebnis: 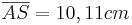 ]
]