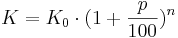Exponential- und Logarithmusfunktion
Exponentialfunktion
| Arbeitsauftrag
Wir betrachten nun als erstes die Exponentialfunktion. Schau dir die Präsentation an, um dir alle Einzelheiten wieder zu aktivieren. |
{{#slideshare:exponentialfunktion-100817023423-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Exponentialfunktionen
Exponentialfunktionen
Die wichtigesten Inhalte des Anschitts II Exponential- und Logarithmusfunktion als Übersicht auf dem folgenden MindMap. Natürlich wieder zum Ausdrucken.
![]() MindMap Exponential & Logarithmusfunktionen
MindMap Exponential & Logarithmusfunktionen
Leerzeile
Aufgaben
Hier warten nun Aufgaben zu Exponentialfunktionen, diese sind auch sehr häufig in der Abschlussprüfugen zu finden!
| Aufgabe 1
Ordne den Funktionsgleichungen ihre Graphen und Asymptoten zu. Los geht's! |
Leerzeile
| Aufgabe 2 Berechnungen zu Exponentialfunktionen. |
Leerzeile
| Karl der Große (742-814) wurde im Jahr 800 römischer Kaiser. Angenommen er hätte in diesem Jahr einen Cent für dich angelegt auf einem Sparbuch. Du bekommst jährlich 2% Zins, der Zinsertrag bleibt auf dem Sparbuch. Wie viel Geld hättest du im Jahr 2010?
|
Leerzeile
Weiter gehts zu Logarithmus
Leerzeile
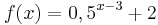
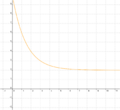
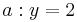
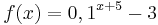
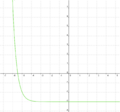
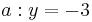
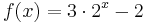
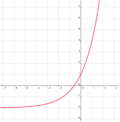
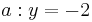
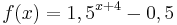
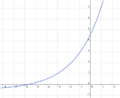
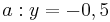
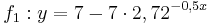 beschreibt welche Spannung y nach x Sekunden an einem Kondensator anliegt. Die maximale Spannung (Sättigungsspannung) ist 7V. Wie viel Prozent der Sättigungsspannung hat der Kondensator nach 2,60s erreicht? (Abschlussprüfung 2004; Aufgabengruppe A; 1.2)
beschreibt welche Spannung y nach x Sekunden an einem Kondensator anliegt. Die maximale Spannung (Sättigungsspannung) ist 7V. Wie viel Prozent der Sättigungsspannung hat der Kondensator nach 2,60s erreicht? (Abschlussprüfung 2004; Aufgabengruppe A; 1.2)