Berechnungen in Dreiecken: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 46: Zeile 46:
  
 
Die gleichschenkligen Dreiecke <math>AB_nC_n \quad</math> bilden eine Dreiecksschar mit dem gemeinsamen Punkt <math>\quad A(0|0)</math>. Auf der Geraden g mit der Gleichugn <math>\quad y=-2x+6</math> liegen die Mittelpunkte <math>M_n(x|-2x+6)</math> der Hyptenusen <math>\quad[AB_n]</math>.
 
Die gleichschenkligen Dreiecke <math>AB_nC_n \quad</math> bilden eine Dreiecksschar mit dem gemeinsamen Punkt <math>\quad A(0|0)</math>. Auf der Geraden g mit der Gleichugn <math>\quad y=-2x+6</math> liegen die Mittelpunkte <math>M_n(x|-2x+6)</math> der Hyptenusen <math>\quad[AB_n]</math>.
−
{|
 
−
|[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']]
 
−
|<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Pyramide.ggb"/>
 
−
</popup>
 
−
|}
 
  
 
<quiz display="simple">
 
<quiz display="simple">
Zeile 66: Zeile 61:
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
  
−
*Zeige, dass für den Flächeninhalt A der Dreiecke <math>\quad AB_nC</math> in Abhängigkeit von der Abzisse x der Punkte M<sub>n</sub> gilt: <math>A(x)=85x²-24x+36)</math>FE
+
*Zeige, dass für den Flächeninhalt A der Dreiecke <math>\quad AB_nC</math> in Abhängigkeit von der Abzisse x der Punkte M<sub>n</sub> gilt: <math>\quad A(x)=85x^2-24x+36)</math>FE
−
<popup name="Tipp"> Suche einfach, Flächengleiche Figuren!
+
<popup name="Tipp"> Suche einfach, flächengleiche Figuren!</popup>
  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
  
 +
<quiz display="simple">
 +
{
 +
| type="{}" }
 
*Die Dreiecke <math>\quad AB_3C_3</math> und <math>\quad AB_4C_4</math> haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C<sub>3</sub> und C<sub>4</sub>.
 
*Die Dreiecke <math>\quad AB_3C_3</math> und <math>\quad AB_4C_4</math> haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C<sub>3</sub> und C<sub>4</sub>.
−
Lösung: C<sub>3</sub>( -6 _3)|( 6 _3) und C<sub>4</sub>( 8,4 _3)|( 1,2 _3)
+
Lösung: C<sub>3</sub>{ -6 _3}|{ 6 _3} und C<sub>4</sub>{ 8,4 _3}|{ 1,2 _3}
 
</quiz>
 
</quiz>
  
Zeile 89: Zeile 87:
 
{|
 
{|
 
|[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']]
 
|[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']]
−
|<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Pyramide.ggb"/>
+
|<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Potenzfunktion_Hyperbelast.ggb"/>
 
</popup>
 
</popup>
 
|}
 
|}
 +
  
 
<quiz display="simple">
 
<quiz display="simple">
Zeile 106: Zeile 105:
 
<math>\overline{QR_n}(\epsilon)=\frac{2,64}{\sin (40^\circ+\epsilon)} cm</math>.
 
<math>\overline{QR_n}(\epsilon)=\frac{2,64}{\sin (40^\circ+\epsilon)} cm</math>.
 
[Teilergebnis: <math>\quad \overline{AS}=10,11cm</math>]
 
[Teilergebnis: <math>\quad \overline{AS}=10,11cm</math>]
−
<popup name="Tipp"> Sinussatz im Dreieck <math>QR_nS</math>
+
<popup name="Tipp"> Sinussatz im Dreieck <math>QR_nS</math></popup>
  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  

Version vom 4. Juni 2010, 20:01 Uhr

Vista-Community Help.png
Lernpfad-Navigator

LERNPFAD

Trigonometrie

Arbeitsauftrag

Die wichtigeste Anwendung von Sinus, Cosinus und Tangens sind Berechnungen an Dreiecken, um Längen und Winkel zu ermitteln. Es gibt Sätze zur Brechnung an

  • rechtwinkligen Dreiecken
  • und allgemeinen Dreiecken.

Mit ihrer Hilfe lassen sich fast alle Längen berechnen, denn alle Figuren und auch Körper lassen in Dreiecke zerlegen!

{{#slideshare:dreiecke-100603045008-phpapp02}}
Leerzeile


Aufgaben

Hier warten nun Aufgaben zu Exponentialfunktionen, diese sind auch sehr häufig in der Abschlussprüfugn zu finden!

Aufgabe 1 Peter Fischer Papier.png

Funktionale Abhängigkeit aus der ebenen Geometrie. ((Abschlussprüfung 2006; Pflichtteil; A2 (verändert)).

Die gleichschenkligen Dreiecke 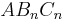AB_nC_n \quad bilden eine Dreiecksschar mit dem gemeinsamen Punkt 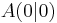\quad A(0|0). Auf der Geraden g mit der Gleichugn 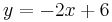\quad y=-2x+6 liegen die Mittelpunkte 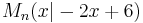M_n(x|-2x+6) der Hyptenusen \quad[AB_n].

1.

*Berechne den Winkel \quad ADM_2, wobei D der Schnittpunkt von g und AC2 ist. Der Punkt C2 besitzt die Koordinaten \quad C_2(3|3).
Lösung: \quad \epsilon=° (2 Nachkommastellen)
Leerzeile
*Die Punkte Cn können in Abhängigkeit der Abszisse x der Punkte Mn dargestellt werden als \quad C_n(3x-6|-x+6). Ermittle die Gleichung des Trägergraphen h der Punkte Cn.
Das Ergebnis kannst du im Applet erkennen, wenn du auf "Trägergraph h einblenden" klickst.

Punkte: 0 / 0

Leerzeile

  • Zeige, dass für den Flächeninhalt A der Dreiecke 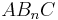\quad AB_nC in Abhängigkeit von der Abzisse x der Punkte Mn gilt: 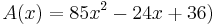\quad A(x)=85x^2-24x+36)FE

Leerzeile

1.

*Die Dreiecke \quad AB_3C_3 und \quad AB_4C_4 haben jeweils einen Flächeninhalt von 36 FE. Ermitteln sie die Koordinaten der Punkte C3 und C4.
Lösung: C3| und C4|

Punkte: 0 / 0


Leerzeile

Aufgabe 2 Peter Fischer Papier.png

Berechnungen an einer Pyramide ((Abschlussprüfung 2006; Pflichtteil; P2).

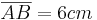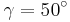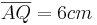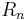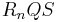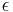Das Quadrat ABCD mit \overline{AB}=6cm ist die Grundfläche einer PyramideABCDS. Die Spitze S liegt senkrecht über dem Eckpunkt A. Der Winkel SCA hat das Maß \gamma = 50^\circ. Der Punkt liegt auf der Kante \quad[AS] mit \overline{AQ}=6cm. Die Punkte \quad R_n liegenauf der Kante \quad [CS], wobei die Winkel \quad R_nQS das Maß \quad \epsilon mit \quad \epsilon > 0^\circ haben.

Hier ist ein Applet zur anschaulichen Darstellung


1.

*Berechnen sie das größmögliche Maß \epsilon.
Lösung: \quad \epsilon=° (2 Nachkommastellen)
Leerzeile
*Zeigen Sie, dass für die Streckenlänge \quad \overline{QR_n} in Abhängigkeit von \quad \epsilon gilt:
\overline{QR_n}(\epsilon)=\frac{2,64}{\sin (40^\circ+\epsilon)} cm.
[Teilergebnis: \quad \overline{AS}=10,11cm]
Leerzeile
*Berechnen Sie das Winkelmaß \quad \epsilon so, dass die Strecke \quad [QR_1] und \quad [QS] gleich land sind.
Lösung: \quad \epsilon=° (2 Nachkommastellen)

Punkte: 0 / 0



Weiter gehts zu Trigonometrische Funktionen Leerzeile


Potenzen und Potenzfunktionen
LERNPFAD | Trigonometrie | Trigonometrische Funktionen | Berechnungen in Dreiecken | Skalarprodukt | Exkurs: Figuren und ihre Eigenschaften
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Prüfungsvorbereitung/Trigonometrie/Berechnungen_in_Dreiecken&oldid=19543“